The Stars at Stake: How the Fight for “Equality” Could Mean the Death of Humanity
In January 2019, a happy, healthy 51-year-old White man called Lee Pomeroy boarded a train for London with his 14-year-old son. He never reached his destination, because en route he got into an argument with a 36-year-old Black man called Darren Pencille. This was a very unwise thing to do, because Pencille won the argument by murdering Pomeroy in a “frenzied attack,” stabbing him “18 times in 25 seconds.”

Lee Pomeroy never reached his destination
This was what I call a “meteor murder.” It flashed through the headlines once when it happened in January and once again when Pencille was convicted in July. Now it’s very likely gone for ever, like many other horrific crimes committed by non-Whites against Whites. There is no mainstream analysis of these crimes and no public lessons are ever drawn from them. Unlike the “racist murder” of the Black teenager Stephen Lawrence, which everlastingly tells us how evil and oppressive Whites are towards non-Whites, the murder of Lee Pomeroy tells us nothing about “race relations.” Absolutely nothing! Lee Pomeroy was a random victim of a misguided fellow human, like the academic Dr Jeroen Ensink, who was stabbed to death by a Black in 2015, or the beautiful White teenager Christina Edkins, who was stabbed to death by a Black in 2013, or the naïve White teenager Mary-Ann Leneghan, who was raped, tortured and murdered by a Black gang in 2006, or the scores or even hundreds of elderly White women raped by a Black gerontophile from 1992 to 2006.
Non-Whites don’t belong in White societies
“There’s nothing to see there, folks! Just move on!” That’s the message of the mainstream media. Of course, the message reverses the truth. There’s an enormous amount to see in such crimes. They form a detailed and extended proof that Blacks and other non-Whites do not belong in White societies and should never have been allowed to enter them. The murder of Stephen Lawrence has been endlessly re-visited in order to promote a giant lie: that wilful White racism explains all non-White failure and dysfunction. The murder of Lee Pomeroy will be forgotten in order to conceal a giant truth: that non-White pathologies arise from non-White genetics and culture, not from White malevolence.
For example, Pencille has been described as a “paranoid schizophrenic,” just like the Black murderers of Dr Jeroen Ensink and Christina Edkins. Rates of paranoid schizophrenia are higher among Blacks, inflicting huge expense on White society even when the Blacks in question don’t take illegal drugs and act violently. But I can see more in Lee Pomeroy’s murder than yet another lesson about non-White genetics and culture. Lee Pomeroy was travelling somewhere on that train. He had a destination and never reached it, thanks to a dysfunctional Black with a history of criminal violence. And so Lee Pomeroy and Darren Pencille may offer us an allegory of the entire human race. A giant task lies before the most intelligent and technologically competent groups of human being. We cannot leave all our eggs in the basket of the planet Earth. We need to get off the planet and establish permanent, self-sustaining bases elsewhere in the solar system and even the galaxy.
America could have been on Mars
This is because humanity could easily be wiped out or plunged back to barbarism by one of the catastrophes that have struck the Earth many times before. It could be an asteroid strike or a giant volcanic eruption or a technological disaster or something huge and deadly that no-one has even dreamt of yet. Like Lee Pomeroy, the White race is travelling somewhere. We have a destination. And I fear that, like Lee Pomeroy, we will never get there, thanks to non-White dysfunction. As the great Paul Kersey of Stuff Black People Don’t Like has put it: “America could have been on Mars!” But America isn’t on Mars. Instead, it has been wasting trillions of dollars on its violent and dysfunctional Blacks: “If you are a white American, over the course of your lifetime the federal government will, on average and on your behalf, transfer $384,109 of your wealth and income to a single black individual.” America is pursuing an illusion: the impossible, illogical and insane goal of “equality.” All other Western nations have wasted huge sums on the same impossible quest.

An asteroid strike could wipe out humanity
But the “Fight for Equality” doesn’t just involve Blacks and other non-Whites. Huge sums have also been spent to rescue women and homosexuals from inequality, oppression and insult. Again, the money has been wasted — in effect, wasted twice over. The money spent pursuing the unachievable goal of equality should have gone on the eminently achievable goal of permanent bases in outer space. We have to get there because we are not safe here. And we could have been there by now, if we weren’t spending so much in the vain pursuit of equality. Indeed, right now we’re spending huge sums to increase the drag on progress and postpone the conquest of space. In Western nations like America, Britain and France, unproductive and unintelligent non-Whites are subsidized with welfare to have more children than productive and intelligent Whites.
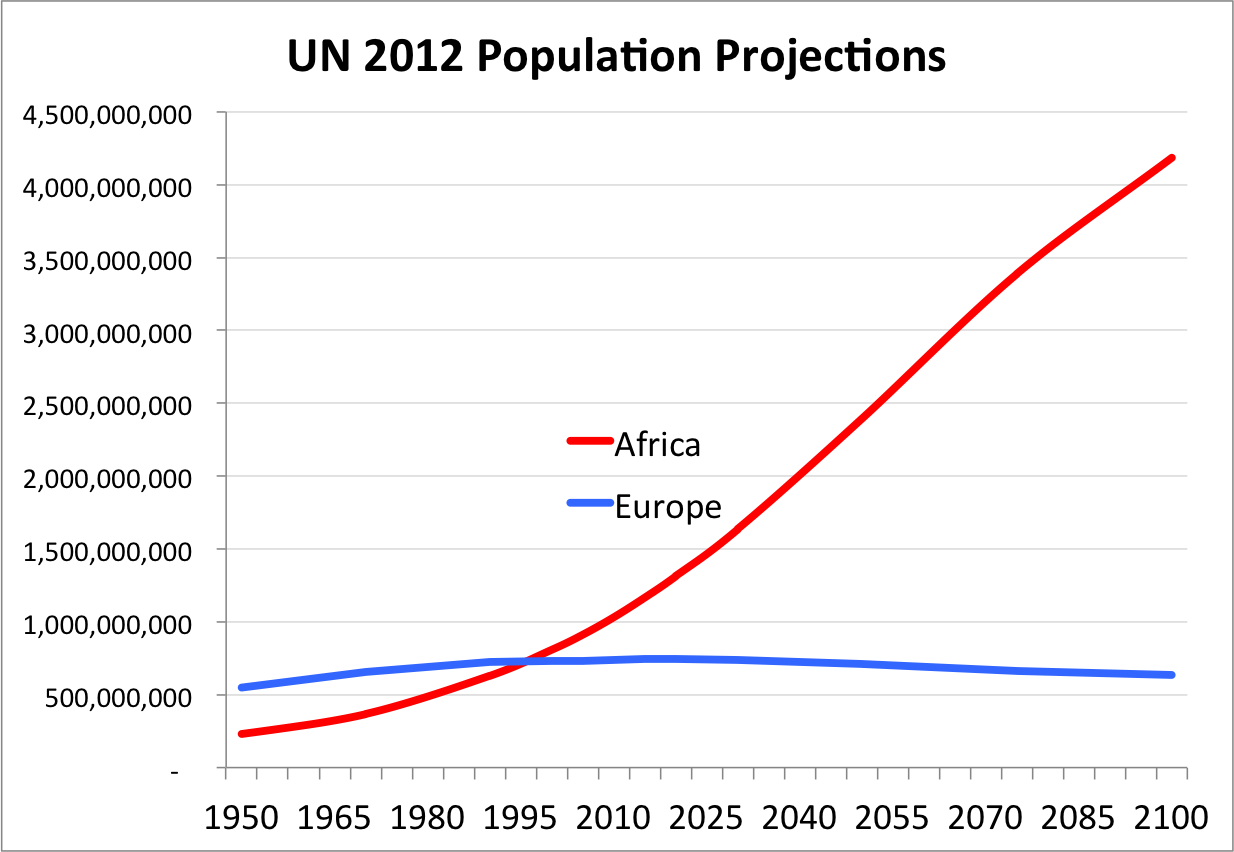
The world’s most important graph
And Steve Sailer has written about “the world’s most important graph,” which shows the soaring population of Blacks in sub-Saharan Africa. That population explosion wouldn’t be happening without Western aid and know-how, but only crime-thinkers like Sailer will point out the enormous dangers of an ever-more populous Africa. Huge numbers of non-Whites want to leave their own corrupt and badly governed nations for the promised land of the West. But Whites will not be able to sustain the Third World if Europe and America are swamped by Third-Worlders. It is lunacy to help unintelligent and unproductive races to reproduce at such high rates. Just look at South Africa: its White minority created and sustained an advanced technological civilization at the tip of a continent whose Blacks were still busy practising witchcraft and human sacrifice.
It’s a Black Thing
While South African Blacks were killing albinos for their magically potent body-parts, South African Whites were building nuclear weapons. That was back in the 1970s, but now Blacks are in charge of South Africa and have had ample opportunity to realize the vast potential seen in them by egalitarians. They haven’t realized it because it doesn’t exist. White South Africans built atom-bombs; Black South Africans rape babies to cure themselves of AIDS. That is where the pursuit of equality leads and that is where the whole West is heading. Meanwhile, the Doomsday clock continues to tick and one or another mega-catastrophe gets closer. And what is America, the world’s most technologically advanced nation, doing about the threat? It’s occupying itself with the vital fight against hair discrimination. In a sick way, it will be funny if the Earth is hit by a big asteroid tomorrow. As the Jewish comedian Mort Sahl may first have joked: “World Ends: Women and Minorities Hardest Hit.” But I’ve never seen a feminist or an anti-racist write about the threat of an asteroid strike or another kind of mega-catastrophe. Why not? After all, women or Blacks or the LGBTQ community could be entirely wiped out or suffer the horrors of a world-wide civilizational collapse.
The trouble is that asteroids and mega-volcanoes aren’t sexist or racist or homophobic. And unlike “climate change,” they’re an entirely natural threat. There are no narcissistic or egotistical rewards in “opposing” a giant lump of speeding space-rock or a toxin-spewing mega-volcano, so the left aren’t interested. Indeed, if it had been up to women and non-Whites, we wouldn’t even know about those threats and the repeated catastrophes that have visited the Earth. Modern science is a White male invention and White men have been the most successful and active explorers of our vast and ancient universe. That’s how we know that it’s also a very dangerous universe. But White men have been so interested in the universe partly because they’re least interested in themselves. That’s been both their strength and their weakness. It’s enabled White men to achieve startling things in science, technology, engineering and mathematics, but also rendered them vulnerable to the self-centred manipulation of feminists, non-Whites and other believers in the Jewish ideologies of “equality” and “anti-racism.”
Dinosaurs didn’t have time
Leftists like those aren’t interested in the universe. They’re interested in themselves. On their own, women and non-Whites would never have discovered the “iridium anomaly” that helped explain the extinction of the dinosaurs. But then women and non-Whites would never have discovered iridium or dinosaurs either. We owe our knowledge of that element and those animals to White men. And those animals offer another allegory of what awaits the human race if the human race continues to pursue equality and confine itself to planet Earth. The dinosaurs were a vast and diverse group of great behavioural and anatomical complexity. Some of them may have been as intelligent as chimpanzees.
The diverse and doomed dinosaurs
And who knows? In time, one or more species of dinosaur might have evolved language and reached human or trans-human levels of intelligence. Rather than White men, it might have been dinosaurs who invented calculus, split the atom and walked on the moon. But dinosaurs didn’t have time for all that. There was a giant space-rock out there with their name on it. When it got here, it wiped out most of them in a single day and all of them (except for the birds) in the months and years that followed. That gave a lowly group known as mammals their chance to take over. And in time, one species of mammal learnt about dinosaurs and the asteroid that had wiped them out.
Self-worship could mean self-extinction
Or rather: one sex of one race of that mammalian species learnt about those things. The species was Homo sapiens, the race was Whites, and the sex was male. Egalitarians won’t like to hear that, but egalitarians don’t like the truth. That’s why they worship the giant lie of equality.
The lie has already killed many Whites like Lee Pomeroy, Jeroen Ensink, Christina Edkins, Mary-Ann Leneghan and Kriss Donald. In the future, it could kill every White on Earth if it prevents us from facing some very big and very definite threats. We have to get off the Earth and out into space. The stars are at stake and “anti-racism” has a truer name than its adherents suppose. By fighting for “equality” and wasting so much money and time, they’re threatening the entire human race.
So are feminists and all other egalitarians. Their self-worship could mean self-extinction. And nobody would be left to appreciate the irony.






There was only one example of sustainable, diverse, safe, prosperous multiracial society. It is South Africa and Rhodesia in the last century
When Blacks and other Non Whites lived under loving care of altruistic White People. And even that relatively successful example did not last long.
Frankly I think asteroid strike is the least of our worries. The more urgent problem is that after majority of population become non White. They will rebuild society in accordance to behavior patterns embedded into their brains by evolution.
Parts of US for example could become “Little Somali” , “Little India” , “Little Mexico” “little Mid-East.”
African cannibals, Indian Thugs, Aztec human sacrificers wielding AK-47, Glocks, Machetes roaming crumbling streets. Slave markets operated by Arabs and Jews etc etc. ,
Parts of the US already have “Little Somalia, Little Mexico, Little Mid-East etc.” And, of course, every Amerikan city has its own “Little Africa” (which is becoming bigger every day). Its just that the continent is large enough to (temporarily) absorb them with less impact on our society at large. However, with the excessively high birthrates of the so-called “minorities”, that change is inevitable and irrevocable.
The first thing I thought about when I saw this case was if Lee Pomeroy had been a basement dwelling alt right loser he would have known to keep his distance and not risk provocation with this man. This is why I openly talk about this stuff with friends and family, and have gotten many angry rebukes. I care about them, so I don’t care if they think less of me in by attempt to lower their risk of getting hurt in such a situation.
I recall reading about ‘quickness to anger’ amongst blacks and the fabled ‘warrior gene’. What is the current state of the art on this area of study? I became aware of the massive violence from blacks in the US via a Bill Whittle video on Ferguson. When the dust settles on this period of history, Obama’s indulgence of ‘the narrative’ could be viewed as a catalysing moment.
You can start on the planet Earth, Antarctica is a depopulated and virgin continent, Japan is already building prototypes of cities under the sea, the Russians have large and modern cities in Siberia, in Brazil Parana state European settlers, led by Britons built Londrina (London in portuges), since to conquer new worlds can take centuries and perhaps it is too late for the white race .. They must be only white settlers.
https://www.youtube.com/watch?v=X6ocw6HxKns
Some remarks :
1) Escape of Whites to another planet is the ultimate “white flight” fantasy, now on a cosmic scale.
2) To be successful, Whites would need to have the courage to reserve such a cosmic flight for Whites only. In other words, they would have to be openly “racist”.
3) But is they choose to be “racist” anyway, they could very well decide to stop and reverse all non-White immigration and reserve their Lebensraum for themselves only.
4) That would be far easier than the problematic colonization of another planet.
5) Even if all the technical problems of the cosmic voyage would have been solved, most likely the prospective planet itself would first need to be made fit for human habitation. This is called “terraforming”.
6) Such terraforming, comprising the formation of an atmosphere, plant and animal life, might take hundreds of thousands, if not millions of years. Not very practical.
7) Even if all these conditions would have been met, there is no guarantee that such a planet is under less danger of a catastrophic meteor impact than the earth. Such risks are cosmic wide.
8) Conclusion : better be “racist” now than trying to escape in cosmic flight fantasies.
Wow, what a rant this is? To bad Tobias you weren’t with me just a couple of months ago and I would have introduced you to a white guy who has three children from three different women none of whom he married. His oldest daughter from his first girlfriend is 13 years old and looking at the guy I gasped and said you must have got an early start you look no more than 21 or 22. He said to me he was 28 years old and is running hiding from his girlfriend who is after him for support and of course his daughter is looking for him? What of the others I don’t know?
[cut]
[mod. note: please try to keep comments short and to the point. More people will read them that way.]
Yes, we all probably know some Whites like that (I even have relatives like that). However, within a civilized society, such behavior is an anomaly which will always exist, albeit on a limited basis. It is as much an anomaly for Whites to have multiple children out of wedlock as it is for Blacks to be married and have only two children, whom they support through long-term, gainful employment.
I live in a city north of Seattle, WA and we have a very large Boeing presence. I live near a big airplane plant that produces twin aisle aircraft..
For 10 years my friends who work at Boeing have been telling me about the companies all out effort to diversify the workforce. So they got rid of tens of thousands of older, mostly white workers and hired in tens of thousands of mostly diverse workers.
Now brand new Boeing planes are dropping out of the sky. Brand new planes. Not one but 2 so far.
I would think that in aerospace competency would be needed more than diversity? But not according to our government and Boeing. A once proud, great company being sacrificed at the altar of diversity.
The last time I flew was from John Wayne Airport to the Grand Canyon, in 1973 [DC-9, Hughes Air West].
In anticipation of this day . . .a culture this/that degenerate deserves no technology and will not be able to keep it. I’ve been awaiting the day for planes to start falling out of the sky- on that day, The West is truly finished.
Also, like so many other companies, Boeing has trimmed its inhouse programming corps in favor of cheaper overseas programming sweatshops, many of them in India. Their work is notoriously shoddy, and the few remaining home-grown programmers are hard-pressed to discover and fix all the bugs. This latest Boeing problem with the 737MAX (or whatever it’s called) was a programming quirk exacerbated by inadequate training for pilots.
Agree or disagree, this is a brave article that says important things.
The mainstream press, even the “conservative” press, would never publish it.
It wasn’t the “unproductive” and “unintelligent” race that infiltrated and subverted America from 19th century. On the contrary, the people who infiltrated and subverted us were highly intelligent and productive.
Jewish immigration has been far more cataclysmic and ruinous for White Europeans than Black immigration.
Even if there was not a single Black in 1865, even if there was no African slavery, Jewish immigrants would’ve invented new – highly compelling and hypnotic – theories on why we should import a 100-million Africans. And they would’ve succeeded just as spectacularly.
Its about loyalty. Jews are intensely loyal to each other. Whereas holier-than-thou Europeans are forever disloyal to each other, chasing senselessly the mirage of abstract “values.”
It’s about loyalty.
South African Whites building an atomic bomb was dandy, Pakistanis and Indians have also built atomic bombs. A better example would have been the world’s first heart transplant, but even that would be objectionable to some, due to: the surgeon being a White male; the recipient being (((Louis Washkansky))) was a “White” male; and donor Denise Darvall a White female. Clearly it was a case of white male misogyny, even though the recipient was at the top of the victim list.
As for “the world’s most important graph”, it is not without irony that a very “old school left” relative of my generation, noted more than 20 years ago, that it was pointless sending aid to Africa, as they continued to breed at a rate where their ecological systems were unable to sustain the size of the populations. Being “old school” meant he opposed immigration as well, and all this before the “immigration gumballs” video was produced. Today, he would be labelled a fascist or neo-Nazi.
“If you are a white American, over the course of your lifetime the federal government will, on average and on your behalf, transfer $384,109 of your wealth and income to a single black individual.” America is pursuing an illusion: the impossible, illogical and insane goal of “equality.” All other Western nations have wasted huge sums on the same impossible quest.”
The question not asked in this article is WHY Western nations have wasted huge sums of money on this impossible quest and at (((whose))) behest?
The key to our awakening and curing of this problem is understanding the pathogen in our midst which herds, guilts and brainwashes us into our suicidal path.
Yes, and why Tobias Langdon has to recommend going to Mars or elsewhere to build an all-white society. Only a very few years ago we had such societies right here on earth, but Tobias Langdon has already given up on getting that back again. Isn’t is just a kind of Churchillian stubborness within his beloved Britain that keeps simple common sense from being recognized?
How did we get so stubborn?!
This is some pedagogy I use to get across the thesis of my 1992 essay, “Race, Gender and the Frontier” without immediately triggering the moral zeitgeist’s the landmines:
Here’s an explanation of the Fermi paradox you won’t see elsewhere:
Harvard’s recent experiment in the evolution of antibiotic resistance graphically shows evolution in action. The frontier of bacteria culture is progressively mutant — to adapt to each new combination of antibiotics. This is common to all life, of course. You can even eliminate the antibiotics and the bacteria, themselves, will evolve the equivalent of antibiotics — but in the reverse of the Harvard experiment.
Here’s how these “antibiotics” evolve in the uniform petri dish:
The frontier culture won’t have to adapt; it’s all just endless agar nutrient out there. By contrast, the bacteria at the origin has to start competing with other bacteria for the remaining nutrients. We’ll call the frontier the “shallow culture” and the origin culture the “deep culture”. Keep in mind that this is a gradient of cultures so please, always interpolate when thinking about the two extrema.
The deep culture evolves to reproduce in the presence of other bacteria and disappearing agar.
If that triggers in your mind an image of cannibalism, you’re right:
The deep culture evolves ways of eating other bacteria since that’s the form in which nutrients appear — not agar. They secrete waste products which, to them, are benign. Parsimoniously, those waste products are toxic to and in-effect digest other bacteria. This is how you arrive at a naturally evolved gradient of “antibiotics” except they are more powerful the deeper into the culture you go: The opposite of the Harvard experiment.
So, recalling that this kind of gradient from deep culture to shallow culture is inherent to the way life itself spreads to through an ecological range and, indeed, to new ecological ranges, such as interstellar space, let’s consider what happens when a species develops the catastrophically rapid form of evolution called “memes” or “culture” in the anthropology sense. For one thing, the shallow culture is most likely to develop technology that deals with differing _natural_ environments in new ecological ranges. It would, therefore, be the culture best adapted to a radical jump to new ecological ranges such as space. The deep culture would be most likely to develop the technology that deals with increasingly competitive _populated_ environments. These technologies can be anything from religion to politics to popular culture. The point being that their coevolved memetic organisms are, like gut bacteria, symbiotic with their own high population density environment. These highly competitive memes are in addition to highly competitive intra-specific genes.
What this means is that before the shallow culture can become spacefaring, it has already gone through a scientific revolution and provided transportation technology orders of magnitude beyond its natural locomotion. At the same time there would be environmental control technologies making the otherwise-marginal ecological ranges far more habitable due to nature-taming infrastructure.
This all-but instantaneously mixes the deep and shallow cultures.
Recall that the deep culture has the ability to essentially “digest” the shallow culture, but not vis-versa.
Indeed, one of the phenomena we should expect to see during this catastrophe is the deeper cultures spawning memes in the form of the arts and religion, including religions posing as intellectual movements if not “sciences”. Upon diffusion into the shallower culture ranges, these memes would express as extended phenotytpes of the deeper culture. Digestion of the shallower culture by these memes would not only divert resources to the deeper cultures, but would use those resources to exponentiate more transport from deeper to shallower culture habitats. None of this requires any conscious memetic engineering. Dawkins blew it when he, in “The Extended Phenotype” refused to even consider the possibility that memes can be extended phenotypes of genes. He admits that “psychological appeal” can be a selective force on memes but fails to recognize that said “appeal” had genetic components. But then, that is an intellectual failure we should _expect_ of shallower culture scientists as the religions posing as “science” overtake the shallower cultures. It’s simply part of the digestion process. As these memes express as extended phenotypes of the deep cultures in the shallow cultures, the shallow cultures should start decaying exponentially with a very short and decreasing half-life. Conversely the deeper cultures should expand exponentially in those frontier ranges until there is catastrophic carrying capacity overshoot — particularly as the technical infrastructure required to support them biologically in those frontier ranges fall apart. The memetic dominance of the deeper culture at this stage guarantees a zero-sum reaction relying on meme wars focused on psychological manipulation.
Proposition: This has wiped out every technological civilization prior to it becoming interstellar.
I recall musing about 35 years ago that the cultural traditions could be literal extensions of DNA.
Then I got into WN and my abstract abilities crashed.
[mod. note: thank you!]
All this is true, but you know what? I’ve spent the past 30+ years begging and pleading with our people, trying to enlighten them to the threats coming their way, by word of mouth, flyers, letters, posters, and now, the internet, and all I’ve ever gotten in return for my attempts is a hatred more hot blooded and feral than any I’ve ever seen our people display towards their true enemies. Somewhere along the way, more than half our people decided to hate themselves literally to death. We can scrutinize the Church, or the oppressive social climate of old peasant Europe which bred long boiling resentment, or the ridiculous excesses and failures of the monarchy, or the numerous class based glass ceilings that kept poor but smart white men stuck in peasant limbo for centuries, but the reality is that this self hatred is probably an amalgamation of all of it, plus some quintessence integral to our people than cannot be properly named, yet simply is, in the same way that a sense of order can be applied to Orientals but cannot be explicitly named or explained.
Whatever the evolution, our people have become our own worst enemy. No one can invade our lands. That’s asinine. The only way the west can ever be conquered is if we LET them in. No dinghy full of black bobbleheads, or troupe of bad attitude tracksuit wearing Mohammads can EVER actually take what belongs to us. It has to be GIVEN to them, and it is. All of it. Given away as if it means nothing. And given away by us, or rather, by the 75% of our own people who either hate themselves to the point of slow suicide, or who are so incredibly naive and pathologically altruistic that they honestly think at some point in these non whites leapfrogging over us, they’ll look back and say, “Hey guys, how’s whitey doing back there?”
It’s been a tough philosophical question for me, how do I begin to care about my people? How much energy and time do I spend on my own people who hate me more than those who wish to destroy them? I have decided, I will continue to fight for my people, just not all of them. Honestly, not even half of them. We are a race within a race at this point, and I consider all those whites who have allowed the situations in the above article to perpetuate to be my enemy, the same enemy as any non white who gives me that look which tells me it’s time to ready my knife hidden in my sleeve.
Your point is succinct and agonizingly veritable and verifiable. As Prof. McD. has said, nothing the Jews have done to us exceeds what we have done to ourselves. And over such a long, long time period.
‘As Prof. McD. has said, nothing the Jews have done to us exceeds what we have done to ourselves’
Pray tell where did he say this?
https://external-preview.redd.it/q1yQUbQ1de8FGO75UyMPcxHtDTMHk7dfBuNs9eW-bpA.jpg?auto=webp&s=28527074c5eae09becaceb12b61ae8f971894a8c
This graphic may help you explain matters to your friends and family. A picture can be worth a thousand words.
To be fair, broad socialization has made it extremely difficult to calculate the economic cost – if any – to the individual of public munificence.
“The only way the west can ever be conquered is if we LET them in”
Once again I raise that little matter of Proposition 187 in California [1994]:
California Proposition 187 (also known as the Save Our State (SOS) initiative) was a 1994 ballot initiative to establish a state-run citizenship screening system and prohibit illegal immigrants from using non-emergency health care, public education, and other services in the State of California. [wiki]
It passed 59-41, losing only in the Bay area of San Francisco and Berkeley. It was declared Unconstitutional by Federal female judge mariana pfaelzer. JEWISH.
So White Will was thwarted by the non-White (((Federal Mafia))).
But we are doing this to ourselves. . .
This notion of people living on some celestial body (whatever it may be) is so ridiculous, I find it almost some kind of trolling game by whoever seriously suggests it.
Can you imagine ‘equality’ so called being pushed upon Eskimo’s in the high north of Canada? Just spend some time thinking about that and the consequences and you’ll truly begin to see and understand the absurdity of our world is reaching some truly astounding proportions and its not going to end well.
If there is one thing that truly sums up mankind’s history it is rape pure and simple. We live to rape the planet, our neighbours, ourselves for gain.
Hosea 4 is interesting in this respect and how it speaks across every generation. Truly timeless. All one needs to do is replace the word Israelites with that of your own people in verse 1 to see and understand the truth of that:
Hear the word of the Lord, you Americans,
because the Lord has a charge to bring
against you who live in the land:
[cut]
a people without understanding will come to ruin!
The UN chart is fanciful and well illustrates the dangers of extrapolation. A toss of Malthus’ die, absent white intervention, will see African populations plummet. Then we can get back to gorging on that sweet Moon cheese.
The vertical scale of the population chart should be logarithmic, showing constant proportional change- 500M, IB, 2B, 4B, 8B, 16B and so on. The chart would then show running out of steam [negroes].
See How to Lie With Statistics [Darrel Huff with (((Irving Geis)))] and others similar.
https://tinyurl.com/y4fyygmu
Respectfully, TJ, such a progression as you have stated is GEOMETRIC, merely doubling. Exponential progression would be 2, 4, 16, 256, etc.
Geometric growth is exponential growth limited to integer cases of the exponent. TJ’s sequence is therefore both exponential and geometric. I don’t know what to call TJ’s sequence but it looks like 2^(2^x) as opposed to 2^x.
Erratum: “I don’t know what to call Poupon Marx’s sequence…”
Sure, but log scale or not, without medical assistance from the West, the next major epidemic will see a vertiginous drop African populations.
How many times does somebody have to stab another human being in the neck to be incarcerated for a few decades? In murderer’s Darren Pencille’s case twice.
Meanwhile, authorities are still scratching their heads – it must be an open sore by now, at the ‘complex’ reasons for this ‘youth’ violence. The achingly globalist minority- (majority in London) worshipping daily newspaper London Evening features news of victims of profoundly senseless murder- most of whom appear to 2nd generation black Africans, with the odd young English man from one of the outer boroughs of London. One such example is Aaron Springer murdered by African Joseph Ankrah in Morden, “Seven years for killer thug who kicked victim like a football”. Yes that’s correct-7 years! How cheap life has become.
In 23rd July Evening Standard a column by a woman called Kavita Puri puts the ‘case’ for an established annual South East heritage month (in the UK). She, Kavita, bases this on her studies and points to a report by the Runnymede (Funnymede) Trust. One line of contention, “From 1948 until 1962 all Indians and Pakistanis were automatically British citizens; came in their thousands to the UK to remake themselves and helped rebuild the country (UK) after the Second World War”. I suggest we use the DNA of some sharp-toothed dinosaurs, artificially rear and clone them because they will a much better job of protecting indigenous British people than our police farce and judiciary.
From:
America and Russia, Part Two: The Far Side of Progress
October 17, 2018
John Michael Greer
The entire narrative of human expansion into outer space is perhaps the most typically Faustian of all our dreams, the ultimate expression of a culture that loves to imagine itself zooming out to infinity in all directions. Scientists have known for decades that it’s not going to happen—outside of the Earth’s magnetosphere, space is so full of hard radiation that prolonged exposure to it will guarantee death by radiation poisoning, and neither the Moon nor Mars nor any other body in the solar system that human beings can visit has a comparable magnetosphere to keep out the lethal rays that stream from the ever-exploding thermonuclear bomb at the center of the solar system. The continuing hold of the myth of space colonization on our collective imagination, in the teeth of such scientific details, may turn out to be the weak point that brings the whole dream crashing down; if it’s not that, though, it’ll be something else.
From:
The Terror of Deep Time
September 20, 2017
John Michael Greer
…What I want to talk about right now is one of the most glaring examples of crackpot realism in contemporary industrial society. Yes, we’re going to talk about space travel again.
No question, a fantastic amount of scientific, technological, and engineering brilliance went into the quest to insert a handful of human beings for a little while into the lethal environment of deep space and bring them back alive. Visit one of the handful of places on the planet where you can get a sense of the sheer scale of a Saturn V rocket, and the raw immensity of the effort that put a small number of human bootprints on the Moon is hard to miss. What’s much easier to miss is the whopping irrationality of the project itself.
(I probably need to insert a parenthetical note here. Every time I blog about the space program, I can count on fielding at least one comment from some troll who insists that the Moon landings never happened. It so happens that I’ve known quite a few people who worked on the Apollo project; some of them have told me their stories and shown me memorabilia from what was one of the proudest times of their lives; and given a choice between believing them, and believing some troll who uses a pseudonym to hide his identity but can’t hide his ignorance of basic historical and scientific facts, well, let’s just say the troll isn’t going to come in first place. Nor is his comment going to go anywhere but the trash. ‘Nuf said.)
Outer space simply isn’t an environment where human beings can survive for long. It’s a near-perfect vacuum at a temperature a few degrees above absolute zero; it’s full of hard radiation streaming out from the huge unshielded fusion reactor at the center of our solar system; it’s also got chunks of rock, lots of them, whizzing through it at better than rifle-bullet speeds; and the human body is the product of two billion years of evolutionary adaptation to environments that have the gravity, atmospheric pressure, temperature ranges, and other features that are found on the Earth’s surface and, as far as we know, nowhere else in the universe.
A simple thought experiment will show how irrational the dream of human expansion into space really is. Consider the harshest natural environments on this planet—the stark summits of the Himalayas; the middle of the East Antarctic ice sheet in winter; the bleak Takla Makan desert of central Asia, the place caravans go to die; the bottom of the Marianas Trench, where the water pressure will reduce a human body to paste in seconds. Nowhere in the solar system, or on any of the exoplanets yet discovered by astronomers, is there a place that’s even as well suited to human life as the places I’ve just named. Logically speaking, before we try to settle the distant, airless, radiation-blasted deserts of Mars or the Moon, wouldn’t it make sense first to build cities on the Antarctic ice or in the lightless depths of the ocean?
With one exception, in fact, every one of the arguments that has been trotted out to try to justify the settlement of Mars can be applied with even more force to the project of settling Antarctica. In both cases, you’ve got a great deal of empty real estate amply stocked with mineral wealth, right? Antarctica, though, has a much more comfortable climate than Mars, not to mention abundant supplies of water and a breathable atmosphere, both of which Mars lacks. Furthermore, it costs a lot less to get your colonists to Antarctica, they won’t face lethal irradiation on the way there, and there’s at least a chance that you can rescue them if things go very wrong. If in fact it made any kind of sense to settle Mars, the case for settling Antarctica would be far stronger.
So where are the grand plans, lavishly funded by clueless tech-industry godzillionaires, to settle Antarctica? Their absence shows the one hard fact about settling outer space that next to nobody is willing to think about: it simply doesn’t make sense. The immense financial and emotional investments we’ve made in the notion of settling human beings on other planets or in outer space itself would be Exhibit A in a museum of crackpot realism.
The barriers to space settlement, even if they had not been conceptually overcome decades ago (ref Gerard O’Neill’s space habitat designs), are subject to potential progress. That would render the notion of space settlement merely speculative, not “crackpot”. Never forget that it was Zubrin, not O’Neill, who set forth the vision of Mars settlement — the strawman you attack. You know who sets up strawmen don’t you?
What is “crackpot” is the conflation of economic feasibility with technical feasibility, as in the argument that various extreme environments on Earth must be settled prior to considering it technically feasible to settle space in the O’Neill sense. Economics has to do with infrastructure build-out, which depends, critically, on the prospects of return on said buildout. If you have one prospect that is a trillion times larger than another, the lesser prospect may never be realized while the greater quite easily realized.
Now, this is not to say that the true destiny of the white race is in O’Neill colonies. I happen to believe it is not even though it could reasonably be argued that I had an influence on Bezos while he was in high school to adopt O’Neill’s vision because I was the Space Studies Institute local support team leader in Miami from 1981 to 1983, doing outreach to local high schools on behalf of O’Neill.
However, O’Neill colonies — or an advance over them — could provide breathing room during a critical time.
Exponentials are powerful.
Yes, making the most of opportunities to establish thriving communities or establishements in our Earth’s challenging environments would be very worthwhile. Manned space travel within our solar system is extremely hazardous and expensive and I don’t see how the enormous costs establishing settlements on Mars, let alone the Moon, would be offset by any gains for a very long time.
I can imagine that the considerable costs setting up bases in various of the Earth’s hostile environments would be worth it in the light of being able to access and use the planet’s hard-to-get resources.
Thank you for that post..
Yes blacks do have a genetic predisposition to violence but whites or at least certain kinds of whites – perhaps Anglo Saxons? – seem to have a genetic predisposition to thinking that all problems have a technological solution. This has got to be one of the nuttiest articles I have read(actually I gave up) anywhere. So once we get rid of our racialist and genderist welfare state in favor of free market capitalism, we are going to spend our surplus going to Mars? This kind of lunacy is why I spent so many years on the Left. It wasn’t all stupidity. How many good old boy techno freaks are lurking in this movement anyway?
Most important chart, according to Sailer. Charts need to show percent changes- a semi-log scale does just that. Each vertical increment will show the identical percentage change. A semi-log chart for African population will show a flattening of the data- soon to be horizontal, meaning no change, implying reduction to follow.
The arithmetic chart makes the situation look far worse than it is- how to lie with statistics.
http://my.execpc.com/~dluisa/ArithVsLog.html
Housing over the last 50 years can be viewed the same ways- arithmetically or logarithmically. The usual arithmetic chart shows strength- the semi-log chart
shows a peaking- the top is basically in. The ability of the Keynesian stimuli
to increase negroes and housing prices has reached its limit- like a drug, larger and larger doses no longer work- even paper money dropped from hellicopters will not work. . .
Modis has written on the S-shaped curve of growth and decay, a couple of good books.
http://www.growth-dynamics.com/
btw Increasing the negro population is a form of inflation- as paper replaced gold, negroes replace Whites- fractional reserve. . .